August 2002

RF Design Tool Matches Two Ports Simultaneously
for Both Active and Passive Devices
by Dale Henkes, Applied Computational Sciences

For many RF and microwave circuits it is important to efficiently transfer the maximum possible amount of power available from a given power source to a load. Often it is necessary to amplify or modify the signal power in some way before it is delivered to the load.

When the signal power travels through a modifying device or sub-circuit, there are two interfaces involved in the power transfer. At each interface where power flows into or out of the circuit (input and output ports) the impedance on one side of the interface must be numerically equal to the complex conjugate of the impedance on the other side or maximum power transfer will not occur as desired. At each interface where the complex conjugate “match” does not exist, an impedance “matching network” must be provided to transform the impedances into the conjugate matched state.

Many circuit simulation programs are available that can analyze a circuit to determine how well it is matched to a given source or load impedance. Computer programs that can only do simulation are sometimes used to design the matching circuits by an iterative process of tuning and optimization. One problem with this approach is that the circuit topology has to be known before it can be presented to the simulator for analysis and subsequent optimization of the component values. Additional problems arise when the designer selects a circuit topology that is incapable of providing the required impedance transformation. The result is a lot of wasted time running an optimization process that never converges to the desired goal.

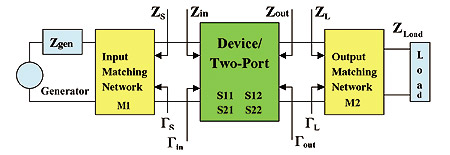
Figure 1: Two-port Impedance Matching

Fewer programs actually provide tools to design the matching networks. Some provide utilities to facilitate the design of a matching network for a single port. But, fewer still provide utilities for designing networks for matching two ports simultaneously. (It will be shown below why this distinction is important). This article describes how the LINC2 design and simulation program from ACS automates the process of designing networks to match both input and output ports simultaneously.

The general problem of impedance matching a device (represented by its two-port S Parameters) to a given source and load termination is shown in Figure 1. The solution, resulting in the overall circuit producing maximum available gain, is an input matching network, M1, and an output matching network, M2, which will provide conjugate matching at both ports simultaneously. However, it should be noted that a conjugate match at both ports can only be achieved if the device is unconditionally stable. In the example in this article, a device will be used that meets this stability criterion.

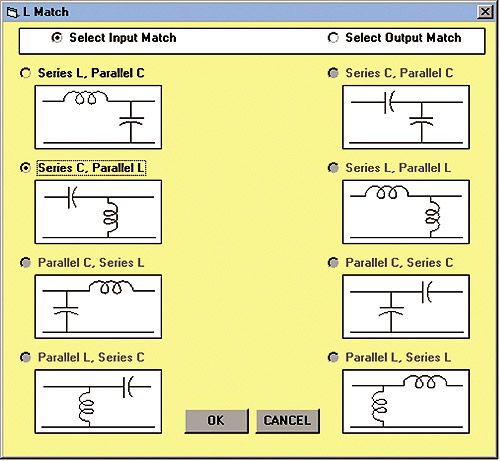
Figure 3: The L-Match Menu

The LINC2 program provides a utility that can be used to automatically solve the matching problem for the general case, where the device is bilateral. In this case S12=0 and Zin and Zout are NOT simply equal to S11 and S22 respectively:

in = S11 + S12 S21 L/(1 - S22 L)
Equation 1

out = S22 + S12 S21 S/(1 - S11 S)
Equation 2

Zin = Z0 (1 + in)/(1 - in)
Equation 3

Zout = Z0 (1 + out)/(1 - out)
Equation 4

The goal is to make ZS = Zin* and ZL = Zout*. The determination of Zin and Zout is required before the matching networks can be designed, but calculation of Zin and Zout is not easy to do manually. The reason is that Zin depends on ZL. But ZL depends on Zout which in turn is a function of ZS which depends on Zin. This is completely circular since we were trying to find Zin in the first place. A similar situation exists when trying to determine the value of Zout. This problem can only be solved by writing two complex simultaneous equations in the variables Zin and Zout. Calculation of Zin and Zout to obtain ZS and ZL is most efficiently done by using a computer program such as LINC2. LINC2 not only finds the ZS and ZL that yield a simultaneous conjugate match but automatically designs the matching networks as well.

Use of the LINC2 tool to design matching networks for an active device was presented in an article in the December 2001 issue of MPD (see “RF Design Software Combines Synthesis and Simulation” on page 12 of the December 2001 issue of MPD). The example in this article will focus on using this tool to design the matching networks for a passive device. The two-port passive device requiring matching to 50 ohms is an IF monolithic crystal filter for 183.6 MHz.

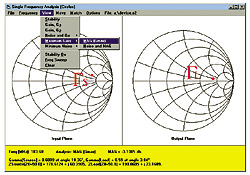
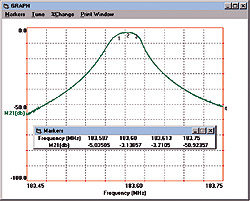
Figure 2: Device Terminations for Simultaneous Matching Click to enlarge	Figure 7: Simulated S21 Click to enlarge
Figure 6: Simulated S11 and S22 Click to enlarge	Figure 8: Measured Zin and Zout Click to enlarge

Design Example– matching a monolithic crystal filter to 50 ohms
The filter in this example was intended for use as an IF filter in an AMPS cellular telephone with an IF frequency of 183.6 MHz. The manufacturer specifies that the insertion loss of the filter will be less than 4.5 dB and that the -3 dB passband edges will be at least +/-13 KHz from the passband center. Additionally, the match at both ports should provide a return loss better than 10 dB (about 2:1 VSWR) over the band defined by 183.6 MHz +/- 11 KHz. There are other specifications, such as stop band attenuation, but we will focus on these three here because these are the ones that we can influence most with our matching networks. Our design goal then becomes:

Filter’s nominal passband center: fn = 183.6 MHz
Insertion loss (IL): 4.5 dB max.
Maximum Passband Attenuation (fn +/- 13 KHz): IL + 3 dB
Match input port to 50 ohms: >10 dB return loss (from 183.589 MHz to 183.611 MHz)
Match output port to 50 ohms: >10 dB return loss (from 183.589 MHz to 183.611 MHz)

The Design Procedure
The design procedure consists of measurement of the device’s S Parameters, synthesis of the matching circuits, simulation of the circuit design, building the prototype, and finally verification through measurement that the hardware meets the design goals. The following steps outline this process:

1. Measure the Device’s S Parameters
Measure the S Parameters of the filter mounted alone on the circuit board without matching networks. (When the S Parameters are available from the device manufacturer this step is unnecessary). Store these “Device” S Parameters on a data disk and transfer to a computer running the LINC2 design and simulation program.

2. Determine the Required S andL from the Device’s S Parameters
Load the device’s S Parameter file into the LINC2 Circles Utility and select “Maximum Gain” from the “View” options. After selecting 183.6 MHz from the frequency menu, the conjugate match points (S and L) will be displayed in the input and output planes respectively as shown in Figure 2. These are the source and load reflection coefficients that will properly match the filter. Their numeric values are printed at the bottom of the screen along with their equivalent impedance values (Zsource and Zload). Although this information is interesting (and even necessary for anyone attempting to design the matching circuits manually) the program does not require the user to do anything with S, L, Zsource or Zload. That is because LINC2 synthesizes the matching circuits automatically (next step in the design procedure).

3. Synthesize the Matching Networks
As shown in Figure 2, the program calculated the optimum source and load terminations required to properly match the device and yield the Maximum Available Gain (MAG). The LINC2 Circles Utility reports that the MAG in this case is -3.14 dB. This suggests that more than 1 dB of margin can be achieved over the insertion loss spec (4.5 dB max). Matching to 50 ohms is assumed by default but this can be changed (from the Options menu) for either or both port 1 and port 2. The next step is to select the desired type of matching networks from a list of available circuit topologies displayed in the “Match” menu. The networks available include “L”, “PI”, “T”, and networks consisting of various distributed (transmission line) elements. In this example the “L” match was chosen as shown in Figure 3.

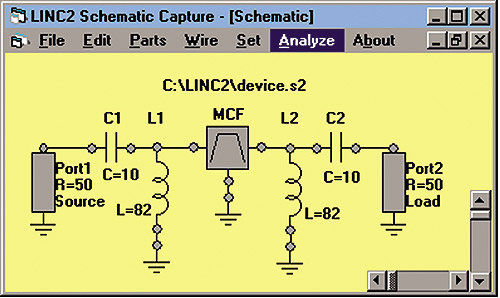
Figure 5: The Circuit Schematic

A palette of all 8 possible “L” configurations are displayed. In this case only two of the 8 “L” networks are capable of solving the given matching problem. The user is guided to the correct choices by making only the valid ones selectable. The two valid choices consist of one low pass and one high pass structure. In this example the high pass structure was selected for both ports. This places an inductor in shunt across the port terminals of the device and has the advantage of utilizing the series capacitor as a DC block as well as a matching component. Clicking “OK” accepts this choice and automatically generates the netlist of the complete filter circuit, including the device and both input and output matching networks as shown in Figure 4. The equivalent LINC2 schematic is shown in Figure 5 with component values rounded to their nearest standard values.

4. Simulate the Completed Circuit
At this point the circuit configuration and all component values have been generated automatically by the LINC2 program. Simulation results can be viewed immediately by selecting “Analyze” from the menu bar in the netlist window (Figure 4- Text Editor). Alternatively, a circuit schematic can be created in the schematic window and the simulation launched from there (Figure 5). In either case the simulation begins by selecting “Analyze” from the menu bar.

                 Figure 4: The Circuit Netlist

5. Compare Simulation Results to Design Goals
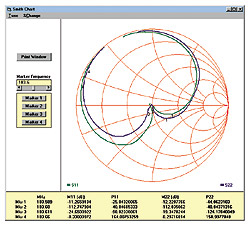
LINC2 facilitates the characterization of circuit performance by offering a variety of methods for displaying simulation data. Data can be displayed in tabulated numerical form or by various graphical methods, including the Smith Chart and Graph windows shown in Figures 6 and 7. In Figure 6 the dB magnitude of S11 is displayed under the heading M11 and its phase under the heading P11. S22 is similarly displayed. Figure 7 is a plot of the dB magnitude of S21 (labeled M21).

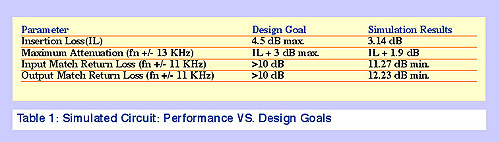
Table 1 summarizes the simulated circuit’s performance and compares it to the design goals. Since all of the design goals listed in Table 1 have been met, the design can proceed to the next step, which is to build the prototype.

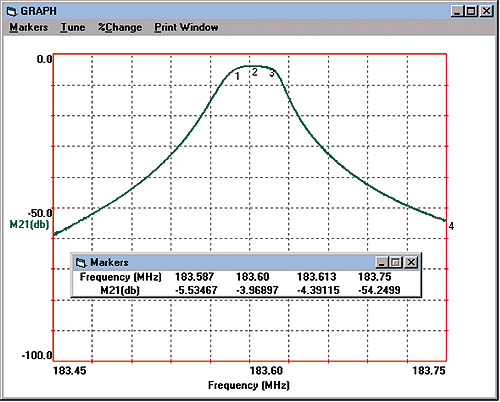
Figure 9: Measured S21

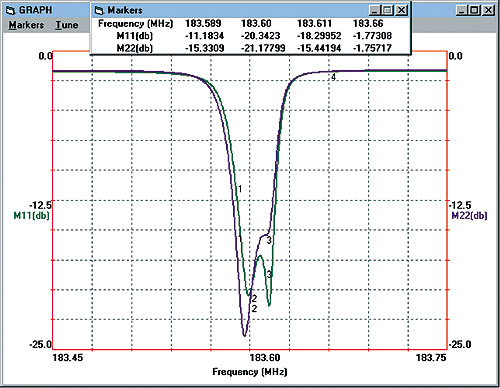
Figure 10: Measured S11 and S22

6. Build and Test the Physical Prototype Circuit
The physical circuit was constructed on a printed circuit board using the components shown in the schematic diagram (Figure 5). The frequency response and the performance of the port matching were measured with an Agilent 8753ES Vector Network Analyzer (VNA). This data was captured from the VNA in an S Parameter file and imported into the LINC2 program for display. 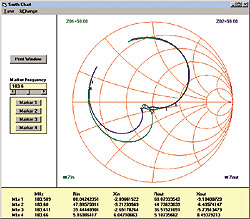The measured data from the 8753ES VNA is displayed in Figures 8, 9 and 10. As indicated in Figure 8, the resistive part of the match at the input and output ports is approximately equal to 48 and 45 ohms respectively with less than 10 ohms of reactance. This results in a return loss of better than 20 dB for both ports at the design frequency of 183.6 MHz (see Figure 10). The minimum return loss over the matching bandwidth (183.589 - 183.611 MHz) is about 11.2 dB as shown in Figure 10. Figure 9 indicates that the insertion loss is less than 4 dB at the nominal center frequency. The maximum attenuation in the passband occurs at 183.587 MHz and is 1.57 dB greater than the insertion loss (difference in S21 between markers 1 and 2 in Figure 9). All of the measured data came in better than the design goal, even though the circuit was constructed with parts having component values equal to the nearest standard values relative to the computer synthesized values and the circuit was not “tuned”.

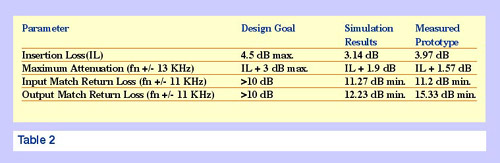
Table 2 summarizes the measured performance of the prototype circuit and compares it to the design goal and simulation results. The prototype circuit met all the design goals on the first cut without tuning. Also, the simulation did an excellent job of predicting the performance of the physical prototype filter circuit.

Although tuning of the matching networks was not required in order to meet the design parameter goals, two small adjustments in component values resulted in a near perfect match at both ports of the prototype circuit. The computer generated circuit called for a 92 nH shunt inductor at the output side of the filter. The nearest standard value of 82 nH was used for this inductor in constructing the physical circuit. Placing a 0.5 pF capacitor in parallel with the 82 nH inductor brought the combined reactance closer to the value calculated by the LINC2 program. Also, the value of the series input capacitor was increased by 10%. With these two changes to the initial prototype circuit, the input and output port impedances improved to Zinput = 49 + J 0.2 and Zoutput = 52 - J 4 ohms respectively. This resulted in measured return losses of better than 36 and 26 dB respectively for the two ports.

“Integrated design environment” are the buzzwords used in the Electronic Design Automation (EDA) software industry today to describe the ability of the software to solve a complex problem or complete a project through the efficient linking of different but related tasks. Beyond the integration of design tools and tasks, the program’s usefulness is enhanced by its ability to interface with the outside environment. LINC2 can export circuit netlist files that can be read by other programs and, more fundamentally, import and export data in industry standard S Parameter files. This allows a convenient interface to RF test equipment in the lab. The usefulness of having an industry standard data interface was demonstrated at both the front end and the back end of this example project. At the start of the project the device data was extracted using a vector network analyzer and imported directly into the program’s matching network synthesis tool. After the prototype circuit was constructed and tested the measured data was returned to the LINC2 program for design verification and documentation. Documenting the prototype’s performance could consist of replicating the instrument’s displays in LINC2 for inclusion into a word processor document (as was done in writing this article). Also, the data can be archived and later recalled by the program for further analysis such as displaying the filter’s group delay or changing the frequency of the marker data readouts.

As shown here, a project can flow smoothly from design to verification using LINC2 because the program couples schematic capture and a suite of RF design tools to a powerful simulator engine. The entire design in this example was completed in a matter of minutes. More information on LINC2 can be found on the Web at www.appliedmicrowave.com.

APPLIED COMPUTATIONAL SCIENCES
Enter Reader Service No. 91